Stack And Queue

Stack And Queue

Stack

Stack is a basic data structure that can be logically thought of as a linear structure represented by a real physical stack or pile, a structure where insertion and deletion of items takes place at one end called top of the stack. 

The basic implementation of a stack is also called a LIFO (Last In First Out) to demonstrate the way it accesses data, since as we will see there are various variations of stack implementations.

There are basically three operations that can be performed on stacks. They are inserting an item into a stack (push), deleting an item from the stack, and displaying the contents of the stack.

Array Representation

•Stack has two variables:
-TOP which is used to store the address of the topmost element of the stack.
-MAX which is used to store the maximum number of elements that the stack can hold.

-If TOP = NULL, then indicates that the stack is empty.
-If TOP = MAX – 1, then the stack is full.

Linked List Representation

A stack can be represented by using nodes of the linked list.

Each node contains two fields : data(info) and next(link)

The data field of each node contains an item in the stack and the corresponding next field points to the node containing the next item in the stack

The top refers to the top most node (The last item inserted) in the stack.

The empty stack is represented by setting top to nut. Because the way the nodes are pointing, push and pop operations are easy to accomplish.

Stack Operation

•push(x) : add an item x to the top of the stack.
•pop() : remove an item from the top of the stack.
•top() : reveal/return the top item from the stack.

Infix, Postfix, Prefix

•Prefix   : operator is written before operands

Example:+7 * 4 5 = 27

•Infix     : operator is written between operands

Example:7 + 4 * 5 = 27
•Postfix : operator is written after operands

Example:7 4 5 * + = 27

Infix Notation

Evaluate a given infix expression: 4 + 6 * (5 – 2) / 3.
To evaluate infix notation, we should search the highest precedence operator in the string.
4 + 6 * (5 – 2) / 3 search the highest precedence operator, it is ( )
4 + 6 * 3 / 3 search the highest precedence operator, it is *
4 + 18 / 3 search the highest precedence operator, it is /
4 + 6 search the highest precedence operator, it is +
10

Postfix Notation

Using Stack
Evaluating a postfix notation can be done in O(N), which is faster than O(N2)

Algorithm:
Scan the string from left to right, for each character in the string:
•If it is an operand, push it into stack.
•If it is an operator, pop twice (store in variable A and B respectively) and push(B operator A).
Pay attention here! It is (B operator A), not (A operator B).
The result will be stored in the only element in stack.

Prefix Notation

Using Stack
Evaluating a prefix notation is similar to postfix notation,the string is scanned from right to left.

Conversion Infix To Postfix

Manually
Algorithm:
1.Search for the operator which has the highest precedence
2.Put that operator behind the operands
3.Repeat until finish

•Manually
•A + B – C x D ^ E / F , power has the highest precedence
•A + B – C x D E ^ / F , put ^ behind D and E
•A + B – C x D E ^ / F , x and / have same level precedence
•A + B – C D E ^ x / F , put x at the end
•A + B – C D E ^ x / F , continue with the same algorithm till finish
•A + B – C D E ^ x F /
•A + B – C D E ^ x F /
•A B + – C D E ^ x F /
•A B + – C D E ^ x F /
•A B + C D E ^ x F / – , this is the Postfix notation

Conversion Infix To Prefix
Manually
Algorithm:
1.Search for the operator which has the highest precedence
2.Put that operator before the operands
3.Repeat until finish

Manually
A + B – C x D ^ E / F
A + B – C x ^ D E / F
A + B – C x ^ D E / F
A + B – x C ^ D E / F
A + B – x C ^ D E / F
A + B – / x C ^ D E F
A + B – / x C ^ D E F
+ A B – / x C ^ D E F
+ A B – / x C ^ D E F
– + A B / x C ^ D E F , this is the Prefix notation

Depth First Search

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.

Queue

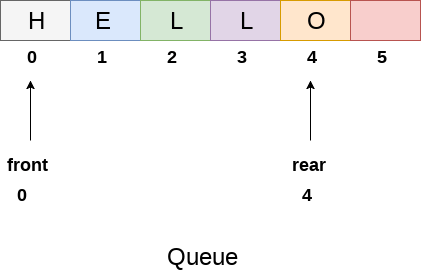
•Queue is an important data structure which stores its elements in an ordered manner.

•Queue can be implemented by either using arrays or linked lists.
•The elements in a queue are added at one end called the rear and removed from the other one end called front.
•The data are stored in First In First Out (FIFO) way, this is the main difference between stack and queue.

Array Representation

Linked List Representation

•In a linked queue, every element has two parts
–One that stores the data
–Another that stores the address of the next element
•The START pointer of the linked list is used as the FRONT
•All insertions will be done at the REAR, and all the deletions are done at the FRONT end.
•If FRONT = REAR = NULL, then it indicates that the queue is empty

Queue Operation

•push(x) : add an item x to the back of the queue.
•pop() : remove an item from the front of the queue.
•front() : reveal/return the most front item from the queue.

Circular Queue

•We can wrap-around index L and R.
•If R reach MAXN then set R as zero, do the same to L.
•It is also known as circular queue.

Queue Applications

•Deques 

is a list in which elements can be inserted or deleted at either end. It is also known as a head-tail linked list, because elements can be added to or removed from the front (head) or back (tail).

•Priority Queues 

A priority queue is an abstract data type in which the each element is assigned a priority.
The general rule of processing elements of a priority queue can be given as:
•An element with higher priority is processes before an element with lower priority
•Two elements with same priority are processed on a first come first served (FCFS) basis 

•Breadth First Search

Breadth First Search (BFS) like DFS is also an algorithm for traversing or searching in a tree or graph. We start at the root of the tree (or some arbitrary node in graph) and explore all neighboring nodes level per level until we find the goal.

Source:

https://en.wikibooks.org/wiki/Data_Structures/Stacks_and_Queues

https://tekslate.com/stack-using-linked-list-in-data-structures