AVL Tree And B Tree
AVL Tree
An AVL tree is a subtype of binary search tree. Named after it's inventors Adelson, Velskii and Landis, AVL trees have the property of dynamic self-balancing in addition to all the properties exhibited by binary search trees.
~ Height of a node:
-The
height of an empty subtree is 0.
-The
height of a leaf is 1.
-The
height of an internal node is the maximum height of its children plus 1.
~Balance factor:
-The
difference height of its LEFT subtree and its RIGHT subtree.
The balance factor of all nodes in
AVL tree should be at most 1.
AVL Tree Example

Right Rotation
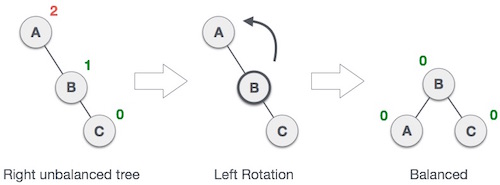
Left Rotation
AVL Insertion Process
If there is an imbalance in left child of right subtree, then you perform a left-right rotation.
If there is an imbalance in left child of left subtree, then you perform a right rotation.
If there is an imbalance in right child of right subtree, then you perform a left rotation.
If there is an imbalance in right child of left subtree, then you perform a right-left rotation.
Rebalance AVL Tree
~There is 4 cases:
-Case 1 : the deepest node is located at the left sub tree of the left child of T.
-Case 2 : the deepest node is located at the right sub tree of the right child of T.
-Case 3 : the deepest node is located at the right sub tree of the left child of T.
-Case 4 : the deepest node is located at the left sub tree of the right child of T.
AVL Tree Rotations
In AVL tree, after performing every operation like insertion and deletion we need to check the balance factor of every node in the tree.
-LL rotation: the new node is inserted in the left sub-tree of the left sub-tree of the critical node
-RR rotation: the new node is inserted in the right sub-tree of the right sub-tree of the
critical node.
-LR rotation: the new node is inserted in the right sub-tree of the left sub-tree of the
critical node
-RL rotation: the new node is inserted in the left sub-tree of the right sub-tree of the
critical node
Deletion
•Delete the node as in ordinary
Binary Search Tree.
•The deleted node will be a leaf or
a node with one child.
•Trace the path from the (parent of)
deleted leaf towards the root. For each node P encountered, check if height of
left(P) and right(P) differ by at most 1.
•If Yes, proceed to parent(P).
•If No, fix sub tree P either by
single rotation or double rotation (as in insertion).
•After we perform rotation at P, we
may have to perform a rotation at some ancestor of P. Thus, we
must continue to trace the path until we reach the root.
Insert:
5,6,7,0,4,3,8
Delete:
3,4,8
B Tree
-B-Tree is defined as a data structure that facilitates faster access of data that are stored in the secondary memory by creating and using indexes for accessing a huge amount of data.
-B-Tree is suitable for creating a dictionary by storing keys and records so that by providing a key, one can access the corresponding record.
Properties of B-Tree
1) All leaves are at same level.
2) A B-Tree is defined by the term minimum degree ‘t’. The value of t depends upon disk block size.
3) Every node except root must contain at least t-1 keys. Root may contain minimum 1 key.
4) All nodes (including root) may contain at most 2t – 1 keys.
5) Number of children of a node is equal to the number of keys in it plus 1.
6) All keys of a node are sorted in increasing order. The child between two keys k1 and k2 contains all keys in the range from k1 and k2.
7) B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward.
8) Like other balanced Binary Search Trees, time complexity to search, insert and delete is O(Logn).
1) All leaves are at same level.
2) A B-Tree is defined by the term minimum degree ‘t’. The value of t depends upon disk block size.
3) Every node except root must contain at least t-1 keys. Root may contain minimum 1 key.
4) All nodes (including root) may contain at most 2t – 1 keys.
5) Number of children of a node is equal to the number of keys in it plus 1.
6) All keys of a node are sorted in increasing order. The child between two keys k1 and k2 contains all keys in the range from k1 and k2.
7) B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward.
8) Like other balanced Binary Search Trees, time complexity to search, insert and delete is O(Logn).
Search
•Because
all data in 2-3 tree are stored in sorted order, searching in 2-3 tree is easy.
We can extend the search algorithm for binary search tree to obtain the search
algorithm in 2-3 tree.
find(ptr, x)
If
ptr is NULL then not found
If
x = A then found
If
x < A then find(ptr->left, x)
If
ptr is 3-node
If
x = B then found
If
A < x and x < B then find(ptr->middle, x)
If
B < x then find(ptr->right,x)
Insert
•Supposed
we want to insert a new data key.
•First
we should find where key should be placed in 2-3 tree using search algorithm,
it will be in one of the leaf.
•If
the leaf is 2-node then simply put the new key
there (so it’s become a 3-node).
•If
the leaf is already a 3-node push the middle data between A, B and key (A and B
are two data in that 3-node) to its parent and split the two remaining data
into two 2-node. Recursively fix the parent.
Deletion
•Supposed
we want to delete a key from 2-3 tree.
•Like
in BST, we should find a leaf key which can replace key we
want to delete. It means deletion always occurs in a leaf node.
•If
the leaf is a 3-node, then delete the key so it becomes a 2-node.
•If
the leaf is a 2-node:
•If
parent is 3-node, get one value from it. If sibling is a 3-node, push one value
of its sibling to the parent (to make the parent 3-node again). If the sibling
is a 2-node, make the parent a 2-node and merge current node with its sibling.
•If
parent is 2-node. If sibling is a 3-node then get one value from parent and
push one value from sibling to its parent. Else merge parent with sibling.
•Fix
parent recursively.
Example
Insert:
5,6,7,0,4,3,8
Delete:
3,4,8


Comments
Post a Comment